MNIST, CIFAR-10 분류 모델 구현하기

-

MNIST

목적

• MNIST 데이터셋을 사용하여 CNN의 학습 설정(batch size, 모델 구조, learning rate)에 따른 성능 변화를 분석
• AlexNet의 주요 기법(ReLU, Dropout, Overlapping Pooling 등)을 적용하여 학습 효율과 과적합 억제 효과를 검증

---

실험 1: BATCH_SIZE 비교

실험 환경

• 모델: SimpleCNN
• 변수: batch size [64, 128, 1024]
• 고정: optimizer=Adam, lr=0.001, epoch=5
• 데이터셋: MNIST (28×28 grayscale) 데이터 분할 및 전처리
  • Train / Validation / Test = 48,000 : 12,000 : 10,000
  • 검증 데이터 비율: 0.2 (20%)

모델 구조

• 입력: (1, 28, 28) MNIST 흑백 이미지
• Conv 블록 1: Conv2d(1→32, 3×3) → BatchNorm → ReLU → MaxPool(2×2)
• Conv 블록 2: Conv2d(32→64, 3×3) → BatchNorm → ReLU → MaxPool(2×2)
• FC 블록: Flatten → Linear(3136→128) → ReLU → Dropout(0.5) → Linear(128→10)
• 출력: (B, 10), softmax는 `CrossEntropyLoss`에서 처리

변수 요약

변수	유형	주요 파라미터	출력 크기
conv1	Conv2d	1→32, k=3, p=1	(B, 32, 28, 28)
pool1	MaxPool2d	k=2, s=2	(B, 32, 14, 14)
conv2	Conv2d	32→64, k=3, p=1	(B, 64, 14, 14)
pool2	MaxPool2d	k=2, s=2	(B, 64, 7, 7)
fc1	Linear	3136→128	(B, 128)
fc2	Linear	128→10	(B, 10)

실험 내용

• batch size 변화에 따른 학습 안정성과 일반화 성능 비교
• step 수 변화가 수렴 속도 및 손실 곡선에 미치는 영향 관찰

실험 상세

Batch Size	Train Accuracy	Validation Accuracy	Train Loss	Validation Loss	Relative Time
64 (녹색)	0.944	0.9895	0.179	0.0375	1.157 min
128 (주황)	0.934	0.9843	0.212	0.0523	1.104 min
1024 (회색)	0.936	0.9832	0.217	0.0574	1.251 min

• Small Batch (녹색)
  • 손실 곡선의 진폭이 크고 진동이 많음 → 학습 과정이 불안정하게 보임
  • gradient noise가 커 다양한 방향으로 탐색하며 빠르게 손실 감소
• Large Batch (회색)
  • 손실 곡선이 부드럽고 진동이 거의 없음 → 학습이 안정적으로 진행
  • gradient noise가 작아 수렴 방향이 일정하지만 탐색 범위가 제한적
  • step 수 감소에도 불구하고 학습 시간 증가
    • 가능한 요인
    • step당 처리 데이터 증가로 인한 메모리 접근 및 I/O 비용 상승
    • GPU 병렬 처리 포화로 인한 커널 실행 순차화
    • CPU–GPU 간 데이터 전송 병목(transfer bottleneck) 발생
    • step 수 감소보다 step당 연산 비용 증가 폭이 더 큼

결론

• 작은 Batch
  • weight 업데이트 빈도가 높아 세밀한 학습이 가능
  • gradient noise가 커서 flat minima 탐색에 유리 → 일반화 성능 우수
  • 손실 곡선의 진동이 크고 학습 안정성이 낮음
  • GPU 자원 활용 효율이 낮아 학습 속도가 느림
  • 불안정한 학습 경향 때문에 작은 learning rate 설정이 적합
• 큰 Batch
  • gradient 계산이 안정적이고 손실 곡선이 부드럽게 수렴
  • 탐색 범위가 제한되어 sharp minima로 수렴할 가능성 있음 → 일반화 성능 저하
  • GPU 자원 활용 효율이 높고 학습 속도가 빠름
  • 안정적인 학습 특성 덕분에 큰 learning rate 적용이 가능
• 종합
  • 작은 Batch: 높은 일반화 성능 / 낮은 안정성
  • 큰 Batch: 높은 안정성 / 낮은 일반화 성능
  • 학습 안정성과 일반화 성능 사이에 명확한 Trade-Off 존재
  • 데이터 크기, 하드웨어 자원, 학습 목적에 따라 Batch Size–Learning Rate 조합을 조정하는 것이 중요

고찰

• LearningRate를 함께 조절하여 비교

---

실험 2: ReLU vs Sigmoid

실험 환경

• 모델: SimpleCNN_Sigmoid (ReLU → Sigmoid 적용)
• 변수: 활성화 함수 [ReLU, Sigmoid]
• 고정: optimizer=Adam, lr=0.001, epoch=5, batch size=64
• 데이터셋: MNIST (28×28 grayscale)
  데이터 분할 및 전처리
  • Train / Validation / Test = 48,000 : 12,000 : 10,000
  • 검증 데이터 비율: 0.2 (20%)

모델 구조

• 입력: (1, 28, 28) MNIST 흑백 이미지
• Conv 블록 1: Conv2d(1→32, 3×3) → BatchNorm → Sigmoid → MaxPool(2×2)
• Conv 블록 2: Conv2d(32→64, 3×3) → BatchNorm → Sigmoid → MaxPool(2×2)
• FC 블록: Flatten → Linear(3136→128) → Sigmoid → Dropout(0.5) → Linear(128→10)
• 출력: (B, 10), softmax는 `CrossEntropyLoss`에서 처리

변수 요약

변수	유형	주요 파라미터	출력 크기
conv1	Conv2d	1→32, k=3, p=1	(B, 32, 28, 28)
pool1	MaxPool2d	k=2, s=2	(B, 32, 14, 14)
conv2	Conv2d	32→64, k=3, p=1	(B, 64, 14, 14)
pool2	MaxPool2d	k=2, s=2	(B, 64, 7, 7)
fc1	Linear	3136→128	(B, 128)
fc2	Linear	128→10	(B, 10)

실험 내용

CNN의 활성화 함수를 ReLU와 Sigmoid로 각각 설정하였을 때 비교

• 학습 속도
• 손실 곡선의 형태
• 최종 정확도 비교

실험 상세

• ReLU (녹색)
  • 손실이 빠르게 감소하며 학습 초반 수렴 속도가 매우 빠름
  • 손실 곡선이 안정적이며 진동 폭이 작음 → gradient 흐름이 원활함
• Sigmoid (보라색)
  • 초기 손실이 크게 시작하며 감소 속도가 느림
  • 손실 곡선의 완만한 감소 → 학습 효율이 낮고 수렴 속도 저하
• Tanh(이미지상 X)
  • ReLU와 크게 차이점 없음

결론

• ReLU(Rectified Linear Unit)
• $f(x)=max(0,x)$
  • 항상 양의 출력을 내보내기 때문에 기울기가 0에 수렴하지 않고 일정하게 유지
  • 비선형성을 유지하면서도 계산이 단순하고, 학습 속도가 빠름.
• Sigmoid
• $f(x)=\frac{1}{1+e^{-x}}$
  • 입력의 절대값이 크면 gradient가 0으로 수렴함
  • 출력이 포화(saturating)되는 구간 발생
  • gradient가 0에 수렴하 gradient vanishing 현상으로 학습이 정체되는 구간 존재

고찰

• 데이터셋 변경 후 Tanh 함수 비교

---

실험 3: Dropout

실험 환경

• 모델: SimpleCNN_Dropout
• 변수: Dropout p [0.0, 0.3, 0.5]
• 고정: optimizer=Adam, lr=0.001, epoch=5, batch size=64
• 데이터셋: MNIST (28×28 grayscale) 데이터 분할 및 전처리
  • Train / Validation / Test = 48,000 : 12,000 : 10,000
  • 검증 데이터 비율: 0.2 (20%)

모델 구조

• 입력: (1, 28, 28) MNIST 흑백 이미지
• Conv 블록 1: Conv2d(1→32, 3×3) → BatchNorm → ReLU → MaxPool(2×2)
• Conv 블록 2: Conv2d(32→64, 3×3) → BatchNorm → ReLU → MaxPool(2×2)
• FC 블록: Flatten → Linear(3136→128) → ReLU → Dropout(p) → Linear(128→10)
• 출력: (B, 10), softmax는 `CrossEntropyLoss`에서 처리

변수 요약

변수	유형	주요 파라미터	출력 크기
conv1	Conv2d	1→32, k=3, p=1	(B, 32, 28, 28)
pool1	MaxPool2d	k=2, s=2	(B, 32, 14, 14)
conv2	Conv2d	32→64, k=3, p=1	(B, 64, 14, 14)
pool2	MaxPool2d	k=2, s=2	(B, 64, 7, 7)
fc1	Linear	3136→128	(B, 128)
fc2	Linear	128→10	(B, 10)

실험 내용

• Dropout 확률을 0.0, 0.3, 0.5로 설정하여 학습 성능 비교
• 동일한 초기 가중치 설정 및 학습 조건 유지
• 각 모델의 학습/검증 손실 곡선 및 최종 Test Accuracy를 비교
• 과적합 억제 효과 및 수렴 속도 차이를 분석

실험 상세

• 초록색: SimpleCNN (Dropout 고정 0.5)
  • 모듈 기반 구조(ReLU·Pool 개별 정의) 연산 그래프가 단순 동일한 드롭아웃 비율임에도 학습 시간이 가장 짧음
• Dropout=0.0 (파랑색): SimpleCNN_Dropout
  • 초기 손실 감소가 가장 빠름.
  • 과적합 억제 장치가 없어서 네트워크가 빠르게 학습함.
• Dropout=0.3 (주황색): SimpleCNN_Dropout
  • 약간 더 느리지만, 여전히 안정적인 감소.
• Dropout=0.5 (회색): SimpleCNN_Dropout
  • 초반 학습 속도가 가장 느림.
  • 절반의 뉴런이 비활성화되어 학습 정보가 줄어들기 때문.

결론

• Dropout 비율에 따라 학습 속도와 일반화 성능 간의 뚜렷한 트레이드오프가 존재.
• Dropout이 낮을수록 초반에 빠르게 손실이 감소
• Dropout이 높은 경우 초반 학습 속도는 비교적 느리지만, 손실 변동이 적고 안정적으로 수렴.

고찰

• 데이터셋을 변경하여 진행해볼 것.
• 가벼운 CNN일 경우 0.5의 Dropout은 학습이 느려지거나 underfitting이 생길 수 있음.

---

MNIST 실험 한계 및 고찰

• MNIST 데이터셋의 특성의 한계
  1. 입력 이미지가 단순함. (28×28, 1채널, 배경 없음)
  2. 클래스 수가 10개로 적고, 각 클래스 간 구분이 명확함.
  3. 데이터 복잡도가 낮아, 기본적인 CNN 구조만으로도 충분히 높은 정확도 달성 가능.
• 약간의 학습 곡선 차이는 존재하지만 크지 않음 > CIFAR-10 데이터셋으로 확장.

Link to original

---

-

CIFAR-10

목적

• CIFAR-10 데이터셋을 사용하여 CNN의 학습 설정에 따른 성능 변화를 분석
• AlexNet의 주요 기법(ReLU, Dropout, Overlapping Pooling, LRN 등)이 CIFAR-10에서 주는 효과를 검증하고자 함

---

공통 실험 환경

• optimizer = Adam(lr=0.001)
• batch_size = 64
• epoch = 10
• 데이터셋: CIFAR-10 (3×32×32 RGB)

실험 1: 활성화 함수별 학습 성능 비교 (ReLU / Sigmoid / _Tanh)

실험 환경

• 모델: SimpleCNN
• 변수: 활성화 함수 [ReLU, Sigmoid, Tanh]
• 고정: optimizer = Adam, lr = 0.001, batch_size = 64, epoch = 10
• 데이터셋: CIFAR-10 (3×32×32 RGB) 데이터 분할 및 전처리
• Train / Validation / Test = 40,000 : 10,000 : 10,000
• 검증 데이터 비율: 0.2 (20%)
• 정규화: 픽셀값 [0, 1] 스케일링

모델 구조

• 입력: (3, 32, 32) CIFAR-10 컬러 이미지
• Conv 블록 1: Conv2d(3→32, 3×3) → BatchNorm → ActivationFn[ReLU, Sigmoid, Tanh] → MaxPool(2×2)
• Conv 블록 2: Conv2d(32→64, 3×3) → BatchNorm → ActivationFn[ReLU, Sigmoid, Tanh] → MaxPool(2×2)
• FC 블록: Flatten → Linear(4096→128) → ActivationFn[ReLU, Sigmoid, Tanh] → Dropout(0.5) →Linear(128→10)
• 출력:(B, 10), softmax는 `CrossEntropyLoss`에서 처리

실험 내용

• 동일한 모델구조를 통해 활성화 함수(ReLU, Sigmoid, Tanh)가 CNN의 학습 성능에 미치는 영향을 비교.
• 모든 실험에서 optimizer는 Adam, 학습률은 0.001, batch size는 64로 고정.
• CIFAR-10 데이터셋을 40,000/10,000/10,000으로 분할하여 학습·검증·테스트에 사용.

실험 상세

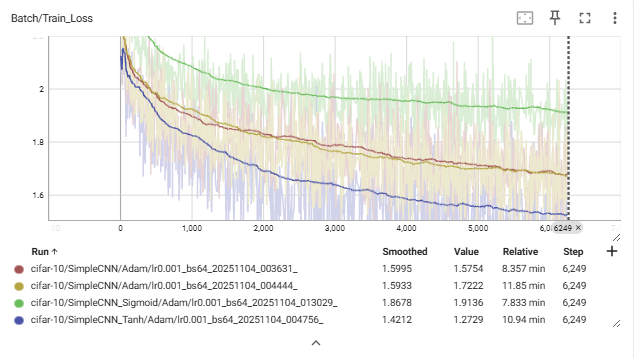
Train Loss 그래프:

• Tanh (파란색) → 가장 빠르게 안정적으로 감소.
• ReLU (빨간/노란색) → 완만하게 감소.
• Sigmoid (초록색) → 감소 정체. Val Accuracy 그래프:
• Tanh > ReLU ≫ Sigmoid
• Tanh는 epoch이 늘어날수록 꾸준히 증가.
• Sigmoid는 거의 향상 없음.

정리

• ReLU (빨간/노란색)
  • 손실 감소가 완만하며, 학습 초반 변동이 존재함.
• Sigmoid (초록색)
  • 손실 감소가 거의 진행되지 않음.
  • 전체 학습 과정에서 정확도 향상 폭이 가장 낮음.
• Tanh (파란색)
  • 손실이 가장 빠르고 안정적으로 감소함.
  • ReLU보다 빠른 수렴을 보이며, 검증 정확도 또한 가장 높음.
• 종합 관찰
  • Tanh > ReLU ≫ Sigmoid 순으로 성능 차이를 보임.
  • 동일한 조건(Adam, lr=0.001, epoch=10)에서도 활성화 함수 선택이 수렴 속도와 최종 정확도에 뚜렷한 영향을 미침.

---

결론

• ReLU가 제일 높은 정확도와 낮은 손실을 기록할거라 예상했지만 본 실험 환경에서는 Tanh가 ReLU보다 낮은 손실과 높은 정확도를 보임.
• 모델의 구조적 한계
  • 낮은 정확도
  • 잘못된 활성화 함수 비교

고찰

• 모델 구조적 한계
  • 모델의 layer가 적어 ReLU의 희소 활성화 특성이 비효율적으로 작용했음.
  • 비선형 표현력이 제한되어 깊은 피처 학습이 어려웠음.
• GPU 사용량 저조(너무 긴 학습 시간)
  • 간단한 모델임에도 학습에 너무 긴 시간이 걸림

---

실험 2: 활성화 함수별 학습 성능 비교 개선된 모델(ReLU / _Tanh)

실험 환경

• 모델: ImprovedCNN
• 변수: 활성화 함수 [ReLU, Tanh]
• 고정: optimizer = Adam, lr = 0.001
• 데이터셋: CIFAR-10 (3×32×32 RGB) 데이터 분할 및 전처리
• Train / Validation / Test = 40,000 : 10,000 : 10,000
• 검증 데이터 비율: 0.2 (20%)
• 정규화: 픽셀값 [0, 1] 스케일링

모델 구조

• 입력 : (3, 32, 32) CIFAR-10 컬러 이미지
• Feature Extractor 블록
  • Conv2d(3→32, 3×3) → BatchNorm → ActivationFn[ReLU/Tanh]
  • Conv2d(32→64, 3×3) → BatchNorm → ActivationFn[ReLU/Tanh] → MaxPool(2×2)
  • Conv2d(64→128, 3×3) → BatchNorm → ActivationFn[ReLU/Tanh]
  • Conv2d(128→128, 3×3) → BatchNorm → ActivationFn[ReLU/Tanh] → MaxPool(2×2)
  • Conv2d(128→256, 3×3) → BatchNorm → ActivationFn[ReLU/Tanh]
  • Conv2d(256→256, 3×3) → BatchNorm → ActivationFn[ReLU/Tanh] → MaxPool(2×2)
• Classifier 블록
  • Flatten → Linear(256×4×4→256) → ActivationFn[ReLU/Tanh] → Dropout(0.5) → Linear(256→10)
• 출력 : (B, 10) – `CrossEntropyLoss` 로 softmax 처리

실험 내용

• 실험 1(SimpleCNN)에서는 Tanh가 ReLU보다 더 높은 정확도를 보였으나, 이는 모델이 얕아서 생기는 문제라 생각됨.
• GPU 사용량이 저조한 것은 과도한 이미지 증강으로 CPU에서 작업이 오래 걸려 병목 생기는 가능성일 거라 생각됨.
• ImprovedCNN은 네트워크 깊이 확장(Conv 6층, 채널 32→256), 데이터 증강의 완화(최적화)를 통해 실험 1의 결과를 재검증하려고 함.

실험 상세

Train Accuracy

• ReLU: 빠르고 안정적인 상승 (최종 0.97 근처)
• Tanh: 학습 속도 느리고 포화 현상으로 0.75 근처에서 정체

Train Loss

• ReLU: 초기 급감 후 0.1 근처에서 안정화
• Tanh: 손실 감소 완만, 진동 폭 큼

Validation Accuracy

• ReLU: 최대 0.88~0.86
• Tanh: 0.74~0.54
  → 실험 1과 달리 ReLU가 역전하여 우세

Validation Loss

• ReLU: 0.55~0.67 근처 안정
• Tanh: 1.0 이상에서 진동 지속

Batch-Level Loss

• ReLU (Batch=512): 가장 빠르고 안정적인 수렴 (최종 손실 ≈ 0.11)
• Tanh (Batch=512): 포화로 인해 손실 0.7 이상 유지
  → ReLU는 batch 크기와 관계없이 일관된 손실 감소를 보임

---

정리

설정	활성화 함수	Batch	Epoch	Train Acc	Val Acc	Val Loss
Adam(lr=0.005)	ReLU	512	100	0.972	0.8858	0.565
Adam(lr=0.005)	ReLU	64	100	0.928	0.855	0.674
Adam(lr=0.005)	Tanh	512	50	0.757	0.749	1.09
Adam(lr=0.005)	Tanh	64	50	0.495	0.543	1.28

• ReLU
  • 빠른 손실 감소 및 높은 안정성
  • 깊은 구조에서 gradient 흐름 유지 → 과적합 없이 높은 일반화 성능
• Tanh
  • 포화 구간 진입으로 gradient vanishing 발생
  • 깊은 층에서 학습 속도 및 정확도 저하

결론

• ImprovedCNN 환경에서 ReLU가 Tanh를 명확히 상회하는 성능을 보임.
• 깊은 구조에서는 ReLU의 비선형성 및 gradient 유지 특성이 강점으로 작용.
• Tanh는 안정적이지만, 깊은 층에서 포화로 인해 학습 효율 저하.
• 실험 1과 달리 구조적 제약이 해소된 환경에서
  ReLU > Tanh 순으로 성능이 역전됨을 확인.

고찰

• 모델의 깊이에 따른 활성화 함수 효율성:
  • 얕은 구조에서는 Tanh의 연속적 활성화가 빠른 초기 수렴을 보일 수 있지만, 깊은 구조에서는 ReLU의 비포화 영역 특성이 gradient 소실을 방지하며 학습 효율을 극대화.
• DataAugmentation은 Dataset에 맞게 사용하기

---

CIFAR-10 실험 이후

• Early Stopping 알아보기
• Dying ReLU 문제 / ReLU 변형 함수 찾아보기
• Precision, F1-score 등 다양한 metric 기법 활용해보기

Link to original

---